代码随想录笔记
2025-06-28 11:08:43 #算法

算法一刷部分笔记 → 代码随想录

链表

1
2
3
4
5
6
// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

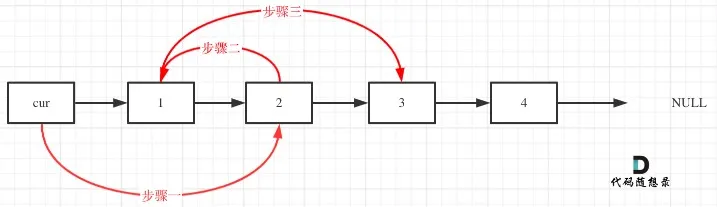
两两交换链表中的节点

  • 不允许交换节点内部的值！
  • 三步交换！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
ListNode *swapPairs(ListNode *head)
{
    if (head == nullptr || head->next == nullptr)
        return head;

    // 设置辅助"头节点"
    ListNode *dummyHead = new ListNode();
    dummyHead->next = head;

    ListNode *p, *l, *r, *temp;

    // 遍历初始化
    p = dummyHead;
    l = head;
    r = head->next;

    while (l != nullptr && r != nullptr)
    {
        temp = r->next; // 辅助节点，防止“断开”

        // 交换相邻节点
        p->next = r;
        r->next = l;
        l->next = temp;

        // 依次遍历
        p = l;
        l = temp;
        if (l == nullptr || l->next == nullptr)
            break;
        r = l->next;
    }

    // 释放空间，返回头节点
    head = dummyHead->next;
    delete dummyHead;

    return head;
}

相交链表

  • 计算链表长度之差
  • 长链表向前遍历差值步
  • 依次遍历以判断链表是否有交点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int numA, numB; // 链表长度
        numA = numB = 0;

        ListNode* p = headA;
        ListNode* q = headB;

        // 计算链表长度之差
        while (p != nullptr) {
            numA++;
            p = p->next;
        }
        while (q != nullptr) {
            numB++;
            q = q->next;
        }
        int diff = numA > numB ? numA - numB : numB - numA;

        p = headA; q = headB;
        // 长链表向前遍历差值步
        if (numA > numB)
            while (diff--)
                p = p->next;
        else
            while (diff--)
                q = q->next;

        // 判断是否相交
        while (p != nullptr) { // 相交 -> 返回交点
            if (p == q)
                return p;
            p = p->next;
            q = q->next;
        }

        return nullptr;
    }
};

环形链表

  • 判断是否有环 -> 快慢指针法
  • 如果有环，利用双指针寻找入环节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
        if (head == nullptr)
            return nullptr;

        // 判断链表是否有环 -> 快慢指针法
        ListNode *slow, *fast;
        slow = fast = head;

        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            if (fast == slow) {
                // 链表有环 -> 利用双指针寻找入环第1个节点
                ListNode* p = head;
                while (p != slow) {
                    p = p->next;
                    slow = slow->next;
                }
                return p;
            }
        }
        // 若程序未在while循环中结束，说明无环
        return nullptr;
    }
};

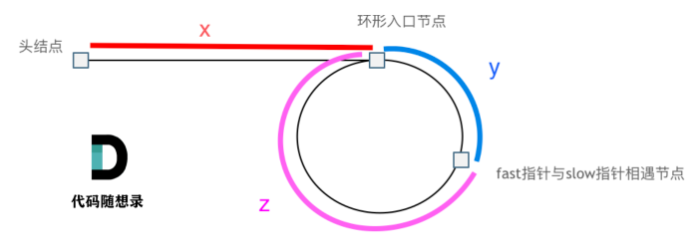
补充：在判断链表有环之后，如何寻找环的入口？
假设从头结点到环形入口节点的节点数为x，环形入口节点到fast指针与slow指针相遇节点节点数为y，从相遇节点再到环形入口节点节点数为 z。
image.png
相遇时slow指针遍历过的节点数为 x + y，fast指针遍历过的节点数为 x + y + n（y + z），n代表fast指针在环内走了n圈才遇到slow指针。注意到fast指针一步走两个节点，slow指针一步走一个节点，则有：
$(x + y) * 2 = x + y + n(y + z) → x + y = n(y + z) (n >= 1).$

  • n = 1时，x = z，即从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点
  • n > 1时，同理！

哈希表

哈希表理论基础

双指针法

双指针法的核心

利用两个“指针”解决问题（反转数组）

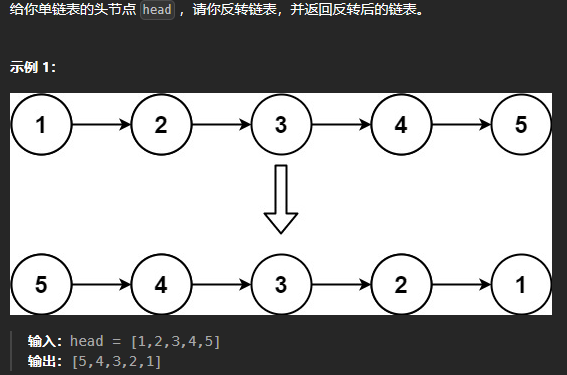
反转链表

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode* reverseList(ListNode* head) {
    ListNode *pre = nullptr;
    ListNode *cur = head;
        
    while (cur != nullptr) {
        ListNode *temp = cur->next; // 辅助节点 → 保存cur的下一节点

        cur->next = pre; // 改变指针方向

        // 更新cur和pre指针
        pre = cur;
        cur = temp;
    }

     return pre; 
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

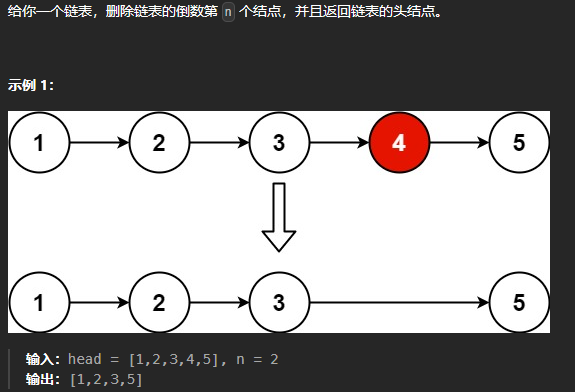
删除链表的倒数第N个结点

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 设置辅助“头节点”
        ListNode* dummyHead = new ListNode();
        dummyHead->next = head;

        // 快慢指针法
        ListNode* slow = head;
        ListNode* fast = head;

        // 辅助指针
        ListNode* pre = dummyHead;

        while (n--) {
            fast = fast->next;
        }

        while (fast != nullptr) {
            pre = pre->next;
            slow= slow->next;
            fast = fast->next;
        }

        // 删除第n个节点
        pre->next = slow->next;
        delete slow;

        // 释放空间，返回结果
        head = dummyHead->next;
        delete dummyHead;

        return head;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

栈与队列

栈与队列理论基础

二叉树

二叉树理论基础

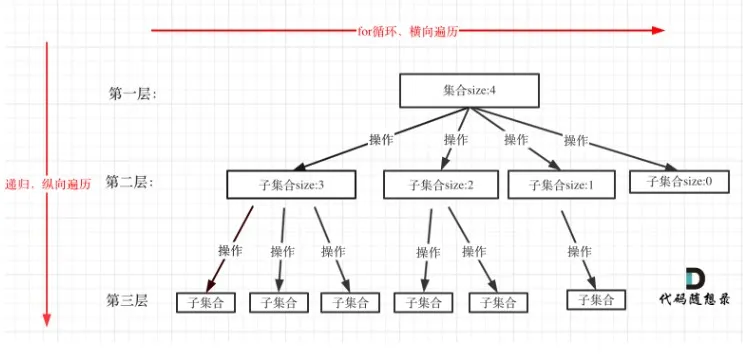
回溯算法

回溯算法的核心

  • 本质上是穷举，筛选所有可能中符合条件的结果
  • 剪枝可以提高效率
  • 回溯可以解决的问题都可以抽象为树形结构

1
2
3
4
5
6
7
8
9
10
11
12
13
// framework of backtracking
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

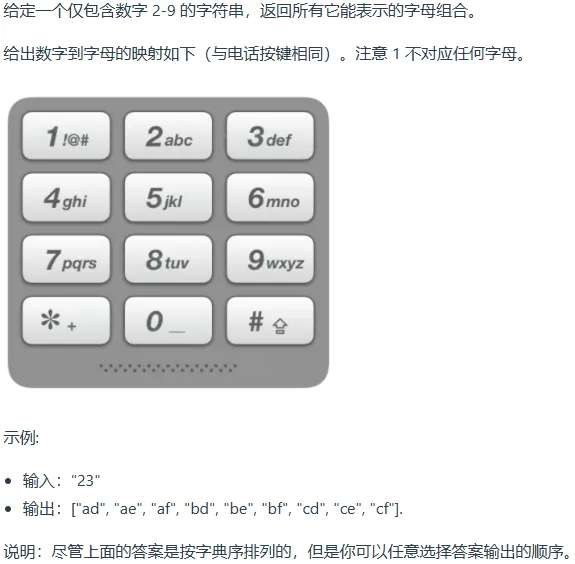
电话号码的字符组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<string> res;
    string str;

    // 字母数字对应表
    const string letterMap[10] = {
        "",
        "",
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
    };

    void backtracking(string digits, int index) {
        if (index == digits.length()) { // 终止条件
            res.push_back(str);
            return;
        }

        int numIndex = int(digits[index] - '0'); // 将index指向的数字转为int
        for (int i = 0; i < letterMap[numIndex].size(); i++) {
            str.push_back(letterMap[numIndex][i]);
            backtracking(digits, index + 1);
            str.pop_back();
        }
    }

    vector<string> letterCombinations(string digits) {
        if (digits.length() == 0)
            return {};

        backtracking(digits, 0); // 回溯

        return res;
    }
};
  • 时间复杂度：O(3 ^ m × 4 ^ n)
  • 空间复杂度：O(3 ^ m × 4 ^ n)
  • m：对应3个字母的数字个数
  • n：对应4个字母的数字个数

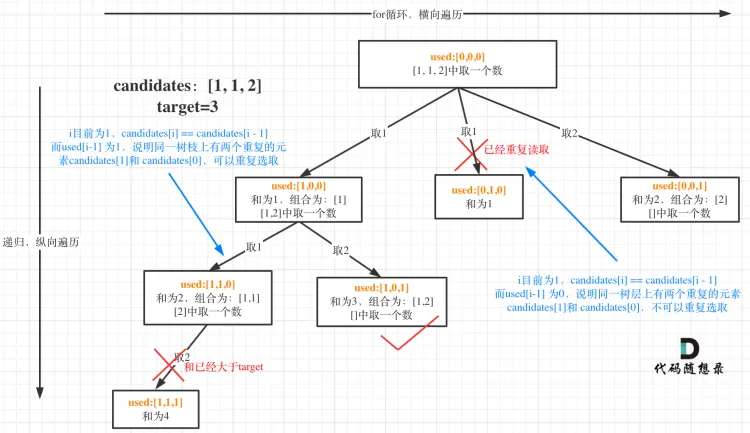
组合总和II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用 一次 。注：解集不能包含重复的组合。
示例

  • 输入：candidates = [10, 1, 2, 7, 6, 1, 5], target = 8

  • 输出：[[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]]

  • used[i - 1] == true → 同一树枝candidates[i - 1]使用过

  • used[i - 1] == false → 同一树层candidates[i - 1]使用过 → 去重！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<vector<int>> res;
    vector<int> vec;

    void backtracking(vector<int>& candidates, int target, int index, vector<bool>& used) {
        if (accumulate(vec.begin(), vec.end(), 0) == target)
            res.push_back(vec); // 终止条件
        
        for (int i = index; i < candidates.size(); i++) {
            // used[i - 1] == true → 同一树枝candidates[i - 1]使用过
            // used[i - 1] == false → 同一树层candidates[i - 1]使用过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false)
                continue;
            vec.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, i + 1, used); // 回溯！
            vec.pop_back();
            used[i] = false;
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        res.clear();
        vec.clear();

        sort(candidates.begin(), candidates.end());

        vector<bool> used(candidates.size(), false);
        
        // 回溯
        backtracking(candidates, target, 0, used);

        return res;
    }
};
  • 时间复杂度：O(n * 2 ^ n)
  • 空间复杂度：O(n)

组合总和：给定一个无重复元素的数组 candidates 和一个目标数 target ，找出candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

  • 与组合总和II 相比，组合总和无需去重！

组合总和III：找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。说明：所有数字都是正整数且解集不能包含重复的组合。

  • 与组合总和相似，亦无需去重！

分割回文串

  • 给定字符串s，请将s分割成一些子串，使每个子串都是回文串，返回s的所有可能的分割方案
  • 输入：s=”aab”，输出：[[“a”,”a”,”b”], [“aa”, “b”]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<vector<string>> res;
    vector<string> path;

    // 判断是否是回文数
    bool isPalindromic(string s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j])
                return false;
        }
        return true;
    }

    void backtracking(const string& s, int startIndex) {
        // 终止条件
        if (startIndex >= s.size()) {
            res.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindromic(s, startIndex, i)) {
                // 获取[startIndex, i]在s中的子串
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            }
            else 
                continue;
            backtracking(s, i + 1);
            path.pop_back();
        }
    }

    vector<vector<string>> partition(string s) {
        res.clear();
        path.clear();

        backtracking(s, 0); // 回溯
        
        return res;
    }
};

非递减子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;

    // 判断序列是否非递减
    bool isIncreasing(vector<int> vec) {
        for (int i = 0; i < vec.size() - 1; i++) {
            if (vec[i] > vec[i + 1])
                return false;
        }
        return true;
    }

    void backtracking(vector<int>& nums, int startIndex) {
        if (path.size() >= 2 && isIncreasing(path))
            result.push_back(path);

        unordered_set<int> uset; // 使用set对本层元素进行去重
        for (int i = startIndex; i < nums.size(); i++) {
            // 去重
            // if (i > startIndex && nums[i] == nums[i - 1]) 
            //     continue;
            if ((uset.find(nums[i]) != uset.end())) {
                    continue;
            }
            uset.insert(nums[i]); // 记录这个元素在本层用过了，本层后面不能再用了
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> findSubsequences(vector<int>& nums) {
        result.clear();
        path.clear();

        backtracking(nums, 0);

        return result;
    }
};
  • 时间复杂度：O(n * 2 ^ n)
  • 空间复杂度：O(n)
  • 若按注释部分的方式去重，则无法对本层元素进行去重，即无法处理形如[1,2,1,1]这样的整数数组！
  • 而用unordered_set进行去重，可保证本层元素不重复，且数组亦可实现此功能（数值范围小的话用数组效率会更高！）

N皇后与解数独

  • N皇后套用回溯框架的思路：在处理节点之前先判断某位置放置皇后是否合理(isValid函数)，其他逻辑相同！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    vector<vector<string>> result;

    // 判断当前棋子摆放是否合理 row -> 行 col -> 列
    bool isValid(int row, int col, vector<string>& chessboard, int n) {
        // 检查列
        for (int i = 0; i < row; i++) {
            if (chessboard[i][col] == 'Q')
                return false;
        }
        // 检查45度角是否有皇后
        for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q')
                return false;
        }
        // 检查135度角是否有皇后
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if (chessboard[i][j] == 'Q')
                return false;
        }
        return true;
    }

    // n -> 输入的棋盘大小 row -> 当前递归到的行数
    void backtracking(int n, int row, vector<string>& chessboard) {
        if (row == n) { // 终止条件
            result.push_back(chessboard);
            return;
        }

        for (int col = 0; col < n; col++) {
            if (isValid(row, col, chessboard, n)) { // 位置合理 -> 放置皇后
                chessboard[row][col] = 'Q'; // 放置皇后
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.'; // 回撤，撤销皇后
            }
        }
    }

    vector<vector<string>> solveNQueens(int n) {
        result.clear();
        vector<string> chessboard(n, string(n, '.')); // 棋盘初始化

        backtracking(n, 0, chessboard);

        return result;
    }
};
  • 解数独错误思路：沿用N皇后代码框架 → 运行结果：直接死循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// row -> 当前递归到的行数
void backtracking(vector<vector<char>>& board, int row) {
    if (row == board.size()) { // 终止条件
        return;
    }

    for (int col = 0; col < board[0].size(); col++) {
        if (board[row][col] == '.') { 
            for (char i = '1'; i <= '9'; i++) {
                if (isValid(row, col, board, i)) { // 位置合理
                    board[row][col] = i; // 放置
                    backtracking(board, row + 1);
                    board[row][col] = '.'; // 回撤
                }
            }
        }
    }
}
  • 问题1：N皇后在棋盘上摆放时，每行只摆放1个皇后，但在解数独问题中，每行不止要填1个数字，因此for循环这一层逻辑只能位于回溯函数内部！
  • 问题2：以上回溯函数的终止条件是参数row遍历至等于board.size()，而某位置可能1~9都无法填入，即回溯可能进行不下去，故无法退出！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    // 判断(row, col)位置填入某个数是否合理
    bool isValid(int row, int col, vector<vector<char>>& board, char val) {
        // 检查行
        for (int j = 0; j < 9; j++) {
            if (board[row][j] == val) 
                return false;
        }
        // 检查列
        for (int i = 0; i < 9; i++) {
            if (board[i][col] == val)
                return false;
        }
        // 检查3 × 3宫内是否合理
        for (int i = 3 * (row / 3); i < 3 * (row / 3) + 3; i++) {
            for (int j = 3 * (col / 3); j < 3 * (col / 3) + 3; j++) {
                    if (board[i][j] == val)
                        return false;
            }
        }
        return true;
    }

    // row -> 当前递归到的行数
    bool backtracking(vector<vector<char>>& board) {
        for (int row = 0; row < 9; row++) {
            for (int col = 0; col < 9; col++) {
                if (board[row][col] == '.') { 
                    for (char i = '1'; i <= '9'; i++) {
                        if (isValid(row, col, board, i)) { // 位置合理
                            board[row][col] = i; // 放置
                            if (backtracking(board)) return true; // 找到最终位置
                            board[row][col] = '.'; // 回撤
                        }
                    }
                    return false; // 某个位置1~9均无法放置，则返回false
                }
            }
        }
        return true;
    }

    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

贪心算法

贪心算法的核心

  • 本质是选择每一阶段的局部最优，从而达到全局最优
  • 难点 → 通过局部最优，推出整体最优
  • 四步骤：划分子问题 → 选择贪心策略 → 求解子问题 → 堆叠全局最优解

无重叠区间

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠！

  1. 按左边界从小到大排序
  2. 从下标1开始，依次判断第i个区间是否于第i-1区间重叠
  3. 若重叠，则需要移除的区间数量加1，且有限保留右区间小的区间（贪心思想：尽可能减小对之后区间的影响）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    // 按照左边界排序
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    }

    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);

        int count = 0; // 统计需要移除区间的最小数量
        for (int i = 1; i < intervals.size(); i++) {
            if (intervals[i][0] < intervals[i - 1][1]) { // 重叠 → 需要移除的区间数自增
                count++;
                // 贪心思想：移除右区间数值较大的区间（这样的区间对之后的区间影响更大）
                intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]);
            }
        }

        return count;
    }
};

跳跃游戏II

  • 若当前覆盖最远距离下标非终点，则步数加一，仍需继续前进
  • 若当前覆盖最远距离下标是重点，则步数无需加一，相当于到达nums[n-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int jump(vector<int>& nums) {
    if (nums.size() == 1)
        return 0;

    int curDistance = 0;    // 当前覆盖最远距离下标
    int ans = 0;            // 记录走的最大步数
    int nextDistance = 0;   // 下一步覆盖最远距离下标
    for (int i = 0; i < nums.size(); i++) {
        nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标
        if (i == curDistance) {                         // 遇到当前覆盖最远距离下标
            ans++;                                  // 需要走下一步
            curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）
            if (nextDistance >= nums.size() - 1) break;  // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束
        }
    }
    return ans;
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

划分字母区间

  • 借助哈希数组以统计每个字母的最远出现位置
  • 遍历字符串，依据哈希数组划分字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> partitionLabels(string s) {
        int hash[27] = {0}; // 哈希数组 -> 用以记录每个字母的最远出现位置

        // 统计各字母出现的最远位置
        for (int i = 0; i < s.size(); i++) {
            hash[s[i] - 'a'] = i;
        }

        vector<int> result;
        result.clear();

        int left = 0, right = 0;
        // 遍历字符串，进行划分
        for (int i = 0; i < s.size(); i++) {
            right = max(right, hash[s[i] - 'a']); // 更新当前片段的右区间
            if (i == right) { // 找到分割线
                result.push_back(right - left + 1);
                left = right + 1; // 更新下一片段的左区间
            }
        }

        return result;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

动态规划

动态规划的核心

  1. 确定dp数组(dp table)以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

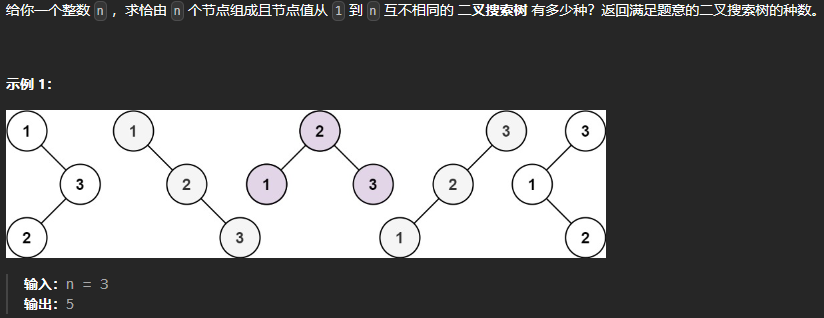
不同的二叉搜索树

image.png

  • n = 3为例，分别考虑头节点为1、2、3时二叉搜索树的数量
  • 头节点为1时，左子树0个节点，右子树2个节点 → dp[0] * dp[2]
  • 头节点为2时，左子树1个节点，右子树1个节点 → dp[1] * dp[1]
  • 头节点为3时，左子树2个节点，右子树0个节点 → dp[2] * dp[0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int numTrees(int n) {
        // dp[i]表示由i个节点组成互不相同的二叉搜索树的数量
        vector<int> dp(n + 1);
        
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
            // i个节点时分别以每个节点为头节点计算二叉搜索树的数量
            for (int j = 1; j <= i; j++) {
                // 以j为头节点时二叉搜索树的个数
                // j - 1: 比j小的节点数 -> 左子树
                // i - j: 比j大的节点数 -> 右子树
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }

        return dp[n];
    }
};
  • 时间复杂度：O(n ^ 2)
  • 空间复杂度：O(n)

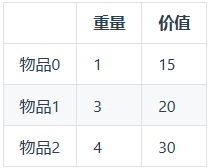
0 - 1背包问题

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大？
image.png

例题

背包最大重量为4
物品为：
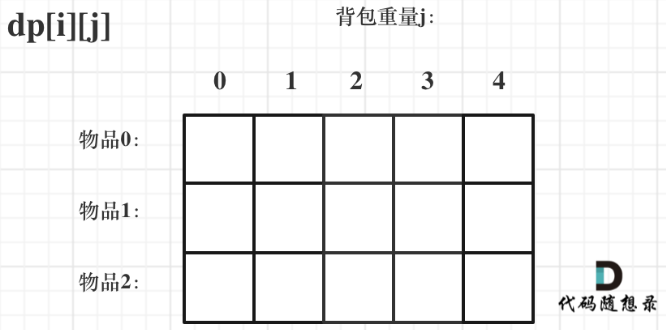
image.png

二维数组解法

  1. 确定dp数组(dp table)以及下标的含义

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少！
image.png

  1. 确定递推公式

遍历dp[i][j]：

  • 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]
  • 放物品i：由dp[i - 1][j - weight[i]] + value[i]推出，dp[i - 1][j - weight[i]]为背包容量为j - weight[i]时不放物品i的最大价值，则dp[i - 1][j - weight[i]] + value[i]就是背包放入物品i得到的最大价值

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

  1. dp数组如何初始化
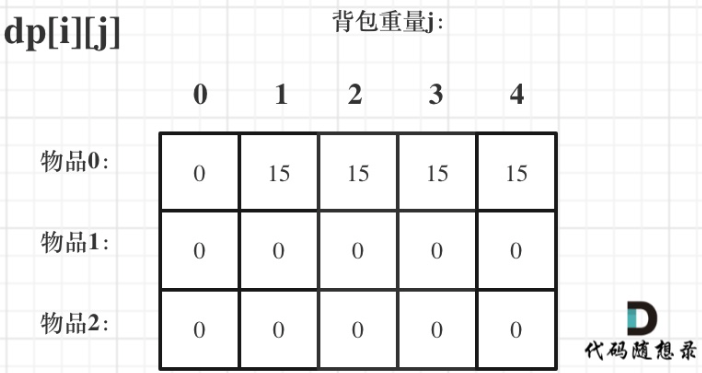
  • 若背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0
  • 若只放物品0，即dp[0][j]，考虑weight[0]和背包容量
1
2
3
4
5
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
}

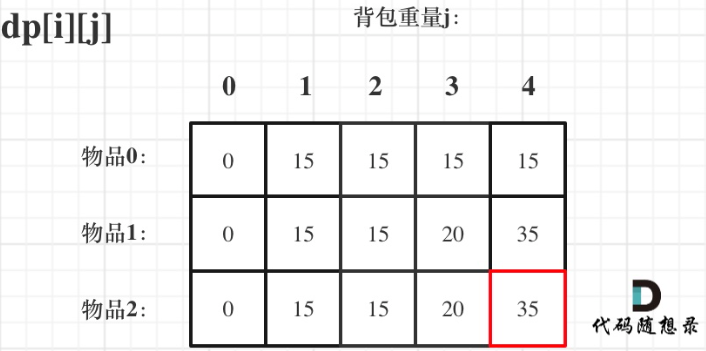
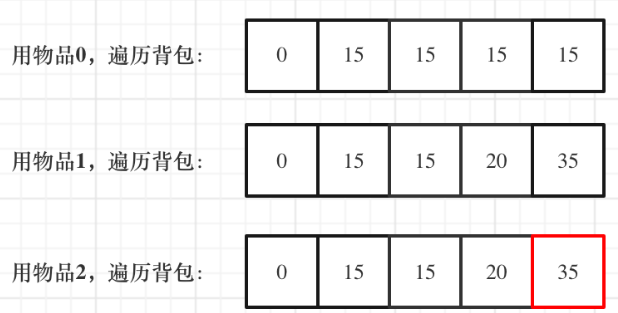
image.png

  1. 确定遍历顺序
  • 先遍历物品和先遍历背包都可以！
  1. 举例推导dp数组

image.png

滚动数组解法

  • 二维数组解法中递推公式为：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
  • 若将dp[i - 1]那一层“拷贝”到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
  1. 确定dp数组(dp table)以及下标的含义
  • dp[j] 表示容量为j的背包能背的最大价值
  1. 确定递推公式
  • dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  1. dp数组如何初始化
  • dp[0] = 0;
  1. 确定遍历顺序
1
2
3
4
5
6
// 倒序遍历保证物品i只被放入一次！
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}
  1. 举例推导dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <vector>
using namespace std;

void test_bag_problem() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化 -> dp[j] 表示容量为j的背包能背的最大价值
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

int main() {
    test_bag_problem();
}

image.png

细节问题

  1. 二维数组实现递推逻辑（两层循环顺序可颠倒）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// weight数组的大小就是物品个数
for (int i = 1; i < weight.size(); i++) { // 遍历物品
    for (int j = 0; j <= bagweight; j++) { // 遍历背包
        if (j < weight[i])
            dp[i][j] = dp[i - 1][j];
        else
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

// weight数组的大小就是物品个数
for (int j = 0; j <= bagweight; j++) { // 遍历背包
    for (int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i])
            dp[i][j] = dp[i - 1][j];
        else
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}
  1. 滚动数组实现递推逻辑时为什么倒序遍历？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// weight = {1, 3, 4}; value = {15, 20, 30}; bagweight = 2;

// 正序遍历 dp[0] = 0;
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagweight; j++) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}
// dp[1] = dp[1 - weight[0]] + value[0] = 15;
// dp[2] = dp[2 - weight[0]] + value[0] = 30;
// 意味着物品0被放入了两次，故无法正序遍历

// 倒序遍历 dp[0] = 0;
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}
// dp[2] = dp[2 - weight[0]] + value[0] = 15; (dp数组初始化为0)
// dp[1] = dp[1 - weight[0]] + value[0] = 15;
// 从后往前循环，每次取得状态不会和之前取得状态重合，保证物品i只被放一次！
  1. 二维数组两层for循环是否可以倒序遍历？

否，滚动数组倒序遍历的本质是遍历二维数组，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍是上一层的，从右向左覆盖

目标和

  • 0 - 1背包原始模型 → “装满背包的最大价值是多少？”
  • 目标和 → “给定背包容量，有多少种方式将背包装满？”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        // 数组元素和为sum，添加"+"的元素之和为left，添加"-"的元素之和为right
        // left = sum - right, right - (sum - right) = target
        // right = (sum + target) / 2
        int sum = accumulate(nums.begin(), nums.end(), 0);

        if ((sum + target) % 2 == 1 || abs(target) > sum)
            return 0;
        
        int bagweight = (sum + target) / 2;

        // dp[i][j]：在数组nums的前i个数中选取元素，使元素之和等于j的方案数
        vector<vector<int>> dp(nums.size() + 1, vector<int>(bagweight + 1, 0));
        dp[0][0] = 1;

        for (int i = 1; i <= nums.size(); i++) { // 遍历物品
            for (int j = 0; j <= bagweight; j++) {
                if (j < nums[i - 1]) // 元素之和 < nums[i]
                    dp[i][j] = dp[i - 1][j];
                else
                    dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];
            }
        }

        return dp[nums.size()][bagweight];
    }
};
  • 时间复杂度：O(n × m)
  • 空间复杂度：O(n × m)

一和零

  • 给定二进制字符串数组strs和两个整数m和n，返回strs的最大子集的长度，该子集中最多有m个0和n个1
  • 输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3，输出：4
  • m和n相当于是一个背包，两个维度的背包
  • 使用二维滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        // 两个维度的0 - 1背包：m个0，n个1   
        // dp[i][j]是指最多有m个0和n个1的最大子集大小
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
        for (string str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0; // 相当于是物品的重量（重量0和重量1）
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            // 遍历背包容量 -> 从后往前遍历
            for (int i = m; i >= zeroNum; i--) {
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

完全背包问题

  • 完全背包与0 - 1背包问题唯一不同的地方是每件物品有无限件！
  • 完全背包的物品可以添加很多次，因此用滚动数组时要从小到大遍历！（0 - 1背包从大到小遍历是为了保证每个物品仅被添加一次）
  • 完全背包问题中先遍历背包容量和先遍历物品均可！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// weight - 物品重量，value - 物品价值 bagweight - 背包容量

// 先物品再背包容量
for (int i = 0; i < weight.size(); i++) {
    for (int j = weight[i]; j <= bagweight; j++) {
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

// 先背包容量再物品
for (int j = 0; j <= bagweight; j++) {
    for (int i = 0; i < weight.size(); i++) {
        if (j - weight[i] >= 0)
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

零钱兑换II

  • 给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
  • 计算组合数 → 外层物品，内层背包容量！
  • 计算排列数 → 外层背包容量，内层物品！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        // dp[j]：装满容量为j的背包的组合数
        vector<int> dp(amount + 1, 0);
        dp[0] = 1;

        for (int i = 0; i < coins.size(); i++) { // 遍历硬币
            for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
};
  • 时间复杂度：O(mn)，其中m是amount，n是coins的长度
  • 空间复杂度：O(m)

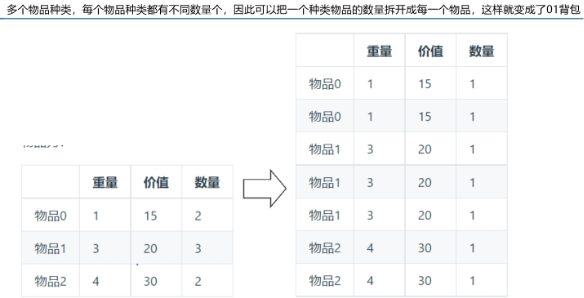
多重背包问题

image.png

打家劫舍 III

  • 小偷发现只有一个入口的可行窃地区，称为root，除了root外，每栋房子有且只有一个“父”房子与之相连。（若两个直接相连的房子在同一天晚上被打劫，房屋将会自动报警）

  • 返回在不触动警报的前提下，小偷行窃能获取的最高金额

  • 输入：[3, 2, 3, null, 3, null, 1]

  • 输出：7（3 + 3 + 1）

  • dp[2]：dp[0]：不偷该节点所得到的最大金钱，dp[1]偷该节点所得到的最大金钱

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }

    // 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* cur) {
        if (cur == nullptr) return vector<int>{0, 0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        // 偷cur，则不能偷左右节点
        int val1 = cur->val + left[0] + right[0];
        // 不偷cur，则可以选择偷左右节点
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度（算上递推系统栈的空间）：O(log n)

买卖股票的最佳时机 III

  • 给定一个数组，它的第i个元素是一支给定的股票在第i天的价格，设计一个算法计算所能获得的最大利润，最多可以完成两笔交易（不能同时参加多笔交易）
  • 输入：[3, 3, 5, 0, 0, 3, 1, 4]
  • 输出：6（第3天购入，第5天卖出；第6天购入，第7天卖出）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        /*
            0 - 没有操作 （其实我们也可以不设置这个状态）
            1 - 第一次持有股票
            2 - 第一次不持有股票
            3 - 第二次持有股票
            4 - 第二次不持有股票
        */
        // dp[i][1]：第i天，买入股票的状态（并不一定是一定要第i天买入股票），此时可获的最大利润
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));

        dp[0][1] = -prices[0]; // 相当于第0天时第一次持有股票，初始化为-prices[0]
        dp[0][3] = -prices[0]; // 同

        for (int i = 1; i < prices.size(); i++) {
            // dp[i][1]: (1)第i天购入股票了，则dp[i][1] = dp[i - 1][0] - prices[i]; (2)第i天未购股票
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            // dp[i][2]: (1)第i天卖出股票了，则dp[i][2] = dp[i - 1][1] + prices[i]; (2)第i天未卖股票
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n × 5)

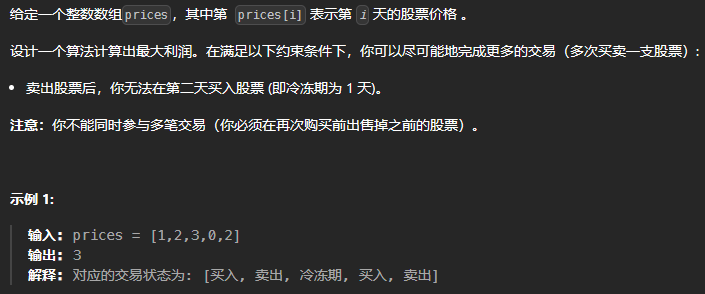
买卖股票的最佳时机含冷冻期

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        /*
            j下标0 - 持有股票状态
            j下标1 - 保持卖出股票状态（但非冷冻期内）
            j下标2 - 今天卖出股票
            j下标3 - 今天为冷冻期
        */
        // 第i天状态为j，所剩的最多现金为dp[i][j]
        vector<vector<int>> dp(prices.size(), vector<int>(4, 0));
        dp[0][0] = -prices[0];

        for (int i = 1; i < prices.size(); ++i) {
            // dp[i][0]:(1)保持购入的状态; (2)前一天为冷冻期或卖出股票状态，更新为购入状态
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
            // dp[i][1]:(1)前一天为卖出股票状态; (2)前一天为冷冻状态
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            // dp[i][2]:前一天必为持股状态
            dp[i][2] = dp[i - 1][0] + prices[i];
            // dp[i][3]:前一天卖出股票 - 状态2
            dp[i][3] = dp[i - 1][2];
        }

        return max(dp[prices.size() - 1][3], max(dp[prices.size() - 1][1], dp[prices.size() - 1][2]));
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

最长重复子数组

  • 给两个整数数组nums1和nums2，返回两个数组中公共的，长度最长的子数组的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int findLength(vector<int>& nums1, vector<int>& nums2) {
    int result = 0;

    // dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度
    vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));

    for (int i = 1; i <= nums1.size(); ++i) {
        for (int j = 1; j <= nums2.size(); ++j) {
            if (nums1[i - 1] == nums2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            if (dp[i][j] > result) // 若出现长度更长的公共数组，则更新
                result = dp[i][j];
        }
    }
    return result;
}
  • 时间复杂度：O(n × m)
  • 空间复杂度：O(n × m)

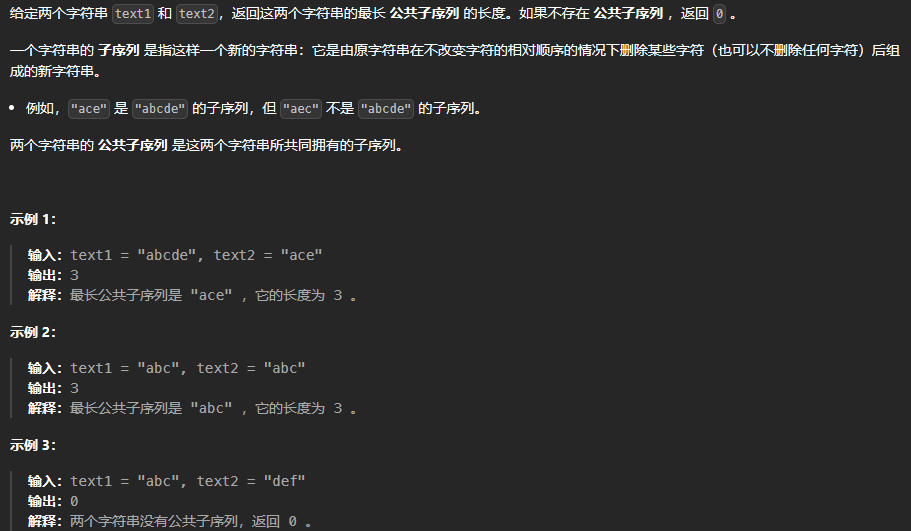
最长公共子序列

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int longestCommonSubsequence(string text1, string text2) {
    // dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列
    vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

    for (int i = 1; i <= text1.size(); ++i) {
        for (int j = 1; j <= text2.size(); ++j) {
            if (text1[i - 1] == text2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1; // 找到了公共元素
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); // 取较大值！
        }
    }

    return dp[text1.size()][text2.size()];
}
  • 时间复杂度：O(n × m)
  • 空间复杂度：O(n × m)

回文子串

image.png

  • 考虑dp数组定义
  • 考虑遍历顺序

完全平方数

  • 给定一个整数n ，返回和为n的完全平方数的最少数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int numSquares(int n) {
        // dp[j]：和为n的完全平方数的最少数量
        vector<int> dp(n + 1, INT_MAX - 1);
        dp[0] = 0;

        for (int i = 1; i <= n; i++) { // 1 - n
            for (int j = i * i; j <= n; j++) { // i * i
                dp[j] = min(dp[j], dp[j - i * i] + 1);
            }
        }

        return dp[n];
    }
};

单词拆分

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        // dp[j]：字符串长度为j的话，dp[j]为true，表示可以拆分为一个或多个在字典中出现的单词。
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;

        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());

        for (int j = 1; j <= s.size(); ++j) { // 遍历背包
            for (int i = 0; i < j; ++i) { // 遍历物品
                string word = s.substr(i, j - i); //substr(起始位置，截取的个数)
                if (wordSet.find(word) != wordSet.end() && dp[i])
                    dp[j] = true;
            }
        }

        return dp[s.size()];
    }
};
  • 时间复杂度：O(n ^ 3)
  • 空间复杂度：O(n)

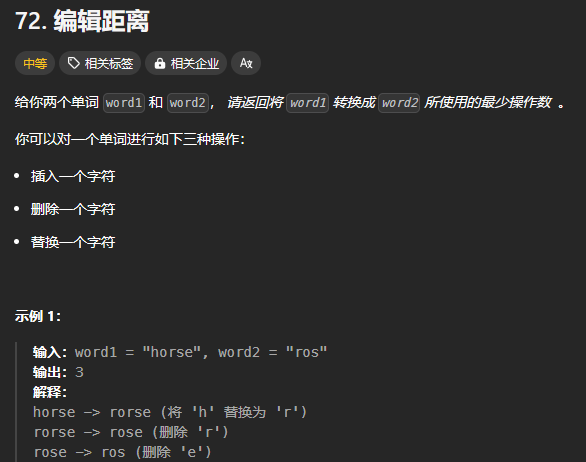
编辑距离

image.png

  • 遵循动规模板即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minDistance(string word1, string word2) {
        // dp[i][j]: 以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2的最近编辑距离
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));

        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;

        for (int i = 1; i <= word1.size(); ++i) {
            for (int j = 1; j <= word2.size(); ++j) {
                if (word1[i - 1] == word2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1; // 增、删、改
            }
        }

        return dp[word1.size()][word2.size()];
    }
};
  • 时间复杂度：O(n * m)
  • 空间复杂度：O(n * m)
Prev
2025-06-28 11:08:43 #算法
Next