位图和布隆过滤器
2025-06-28 14:31:24 #C++

为什么需要位图？

假设我们有1千万个不同的整数需要存储，每个整数的大小范围是1到1亿。然后，给定任意一个整数X，我们需要判断X是否在刚才的1千万个整数内。这个问题该如何处理呢？

常规的做法肯定就是先考虑如何存储这1千万个整数，int类型是4字节，可以表示的范围区间是-2147483648~2147483647，所以每个整数都用int来表示是可行的，约需要38.15MB。

位图

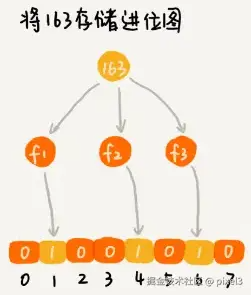
位图其实就是哈希的变形，同样通过映射来处理数据，只不过位图本身并不存储数据，而是存储标记，通过一个比特位来标记这个数据是否存在，1代表存在，0代表不存在。

位图通常情况下用在数据量庞大，且数据不重复的情景下判断某个数据是否存在。

Bytes表示字节，一个字节等于8bit，如果用1个bit来表示一个整数是否存在，那么对于1千万个整数，每个数的范围从1到1亿，就需要1亿个bit，则需要100000000 / 2 ^ 3 / 2 ^ 20，约11.92MB。

位图接口及C++手撕

bitset提供的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
#include <bitset>
using namespace std;

int main()
{
	bitset<8> bs;
	bs.set(2); //设置第2位
	bs.set(4); //设置第4位
	cout << bs << endl; //00010100
        cout << bs.test(2) << endl; //1
        cout << bs.test(6) << endl; //1
	bs.reset(); //清空所有位
	cout << bs.none() << endl; //1
	return 0;
}

自己实现：

  • N = 10000000，即表示该位图可以存储0 ~ 9999999的整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <vector>
#include <iostream>

template<size_t N>
class bitset
{
public:
	bitset() // 开辟空间，向上取整保证足够！
    {
        _bs.resize(N / 32 + 1, 0);
    }

	void set(size_t x)
    {
        size_t i = x / 32; // 处于数组的第几个空间
        size_t j = x % 32; // 处于数组的第几个比特位

        _bs[i] |= (1 << j);
    }

	void reset(size_t x)
    {
        size_t i = x / 32;
        size_t j = x % 32;
    
        _bs[i] &= (~(1 << j));
    }

	bool find(size_t x)
    {
        size_t i = x / 32;
        size_t j = x % 32;
     
        return _bs[i] & (1 << j);
    }

private:
	std::vector<int> _bs;
};

位图的应用场景

  1. 快速查找某个数据是否在一个集合中：一堆32位的整数，怎么判断某个数字在这堆数中是否出现过？
  2. 求两个集合的交集std::bitset<N> intersection = bitmapA & bitmapB;、并集std::bitset<N> unionSet = bitmapA | bitmapB;等。
  3. 操作系统中磁盘块标记：标记使用状态（已分配或未分配）。

位图的优缺点

  • 位图适合密集型数据的存储和查询，空间复杂度很低！

  • 稀疏型数据查询会比较慢（比如查 0~10000 范围存在位图中的数据，实际上只存在 3333 和 9999，会有很多无用查询） -> 优化思路：多级索引位图，将整个位图划分为多个小块，为每个块维护一个索引（标志位） ，查询时，先检查索引确定哪些块包含有效数据，再去子块查询。

布隆过滤器

位图也不是万能的，倘若我们需要存放的1千万个整数的范围是1到100亿怎么办，按道理说，我们申请一个包含100亿个bit的数组就可以了，也是需要1.16GB，太大了，这也是很多电脑和手机承受不起的，那怎么办呢？

布隆过滤器就是让我们有办法在原来12.5MB的内存空间下，使用1亿个bit来存放原本需要100亿个bit才能解决的问题。我们的核心思想就是使用hash函数，把1到100亿大小的数值映射到1到1亿个bit内。

  • 用哈希表存储，缺点：浪费空间。
  • 用位图存储，缺点：不能处理哈希冲突。
  • 将哈希与位图结合 -> 布隆过滤器。

布隆过滤器原理

布隆过滤器（Bloom Filter）是一种用于高效判断一个元素是否属于一个集合的概率型数据结构，它基于位图（Bitmap）的概念，但使用了多个哈希函数来实现更高的查找效率。

布隆过滤器由一个位数组和多个哈希函数组成：初始时，所有位数组的值都被设置为0

  • 当要向布隆过滤器中插入一个元素时，该元素经过多个哈希函数的计算，得到多个哈希值，然后将对应的位数组位置设置为1
  • 当需要判断一个元素是否在集合中时，同样经过多个哈希函数的计算，检查对应的位数组位置是否都为1
  • 如果有任何一位为0，则可以确定该元素不在集合中；如果所有位都为1，则表示该元素可能在集合中（存在误判的概率）。

海量数据处理

  1. 给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

位图。

  1. 给定100亿个整数，设计算法找到只出现一次的整数？

两个位图，同样的两个位图对应的映射的数的位置共同表示映射状态：0次 - 00，一次 - 01， 两次 - 10。

  1. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

两个位图，对两个文件进行分别遍历文件读取数据映射到位图上，然后对位图进行遍历求交集，同一个位置都为1，那么则为交集。

  1. 1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数？

使用两个位图，同样的两个位图对应的映射的数的位置共同表示映射状态：0次 - 00，一次 - 01， 两次 - 10， 三次以上 - 11。

  1. 海量数据分布在100台电脑中，想个办法高效统计出这批数据的TOP10？

对于每一个电脑，都构建一个大小为10的堆(选大的构建小堆，选小的构建大堆)，选出当前电脑的TOP10，接着将所有电脑的数据汇总起来，共1000个数据，继续用堆从其中选出TOP10。

Prev
2025-06-28 14:31:24 #C++
Next